SIZES AND DISTANCES
IN THE SUN-EARTH-MOON SYSTEM:
An Introductory Astronomy Lab

Rung 3: The Distance to the Sun

Aristarchus also came up with a method for finding the distance to the Sun relative to the distance to the Moon. This method once again relies on a particular model for the Sun-Earth-Moon system. In particular, we can no longer assume the Sun to be very far away in the sense that we did for the previous two rungs of our distance ladder (we essentially assumed the Sun to be infinitely far away). What we are relying on is that the Sun's rays do not hit both the Moon and the Earth at the same angle, that the rays are not parallel over the Earth-Moon distance. This difference in the angle that the Sun's rays hit the Moon versus the angle they hit the Earth is very small and this is the reason why this was a particularly difficult measurement for Greek Astronomers to perform. It is important to understand that even though Aristarchus' estimate of the distance to the Sun relative to the distance to the Moon was wrong by a factor of 20, his basic method was correct. Our model now reads:

1. The Earth is a sphere.

2. The Sun may be far away, but close enough that its rays
hit the Earth and Moon at slightly differing angles.

3. The Moon orbits the Earth.

This new model and how it can be used to determine the distance to the Sun can be understood by looking at the following diagram:
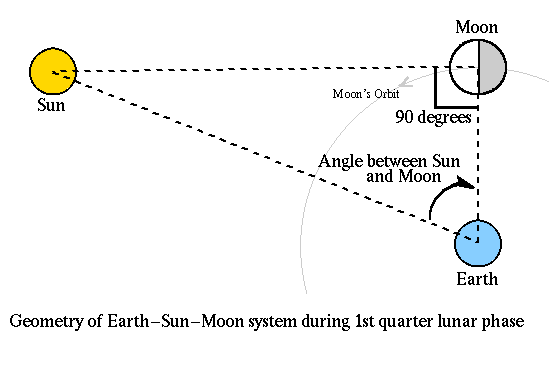Note that when the moon is seen to be exactly in the first quarter phase, the Sun-Moon-Earth angle is a right angle, or 90 degrees. If we can measure the angle between the Sun and the Moon when it is precisely in its first quarter phase (or third quarter, it doesn't matter which) then we can determine the distance to the Sun. We know the distance from the Earth to the Moon, we determined that in rung 2 of our distance ladder. This gives us one side and one angle (the measured angle between the Sun and the Moon) of a right triangle so that we can use trigonometry to determine the length of the hypotenuse, the distance to the Sun. 
                                     distance to the Moon (adjacent)
COSINE(Angle between Sun and Moon) = --------------------------------
                                     distance to the Sun (hypotenuse)
There are two things which make this difficult to carry out. First of all, the Sun is still quite far away, so that the angle measured between the Sun and Moon at first quarter phase is very nearly 90 degrees. The second problem is that it is hard to determine when the moon is exactly in first quarter phase.

With precise observations made at first quarter lunar phase, a Sun-Moon angle of 89.853 degrees is measured.

Question 14: Use the above formula, the angle between the Sun and the Moon given above, and the distance to the Moon from rung 2 to determine the distance to the Sun.

Distance to the Sun = ___________________ km.

Now that we have an estimate for the distance to the Sun it is also possible to determine the diameter of the Sun in kilometers. We know that the angular diameter of the Sun is almost the same as the Moon, about 0.5 degrees on the sky, the most dramatic evidence of this being during a total solar eclipse as shown below.

Question 15: Using the distance to the Sun determined above and the angular diameter of the Sun, which is 0.5 degrees, determine the radius of the Sun in kilometers. Hint: recall the way in which you calculated the distance to the Moon from an estimate of its radius in kilometers (see hint from Rung 2).

Radius of the Sun = ___________________ km.